'Precision' is an adjustment to the Q variable used in GEDmatch's statistics for determining what is a match. Precision=7 is the default setting. Much occurs over short segments, and at P=7, much of this fine detail is rejected in calling probable matches. Statistical considerations in calling matches include what gaps in the SNP sequence are tolerated, and also where the segment boundaries are (ie do they include the last common SNP or go to the next). These considerations are matters for judgement by QEDmatch in formulating its statistical routines. GEDmatch gave no advice on the topic of coincident overlapping match boundaries - perhaps because the definition of a match boundary is somewhat arbitrary as indicated. For our purposes below all that matters is that GEDmatch employs its criteria consistently.

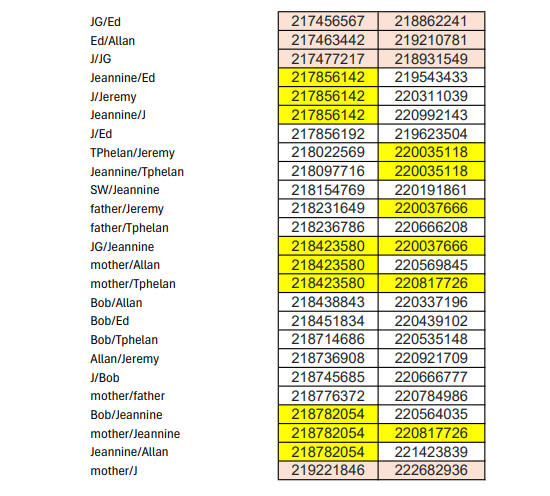
Below we can see more matches at P=3, even if we exclude the potential non-overlaps. The doubled number of matches shows a dramatic enhancement of the number and type of coincident segment boundaries. Though in the context of coincident segment boundaries it might be argued that Types 1 & 2 are not hugely significant in that if IBS matches occur then a coincident segment boundary will arise under the same conditions as an IBD match - because where the common match has the shortest segment then it will generate coincident boundaries in the 2 (Type 1) or 3 (Type 2) segment matches.

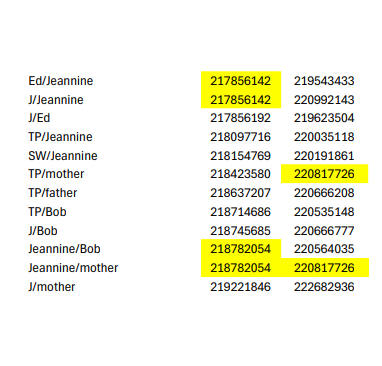
But a moment's thought shows how unusual Types 3 & 5 are. For they show a coincident boundary involving 4 separate people in 2 cases (father/Jeremy/JG/Jeannine at 220037666 and JG/Jeannine/mother/Allan at 218423580). As the number of SNPs for our 3cM segment length is around 300, there will be less than a 1/100 chance for a single coincidence of this sort, and less than 1/10000 for 2. Accordingly our match pattern is extremely unlikely to be IBS. We also see that the 220817726 match links the 218782054 match to the 218423580 and 220037666 coincident matches just discussed.

The Type 4 case shows J and Jeannine have independent matches both sharing the 217856142 segment boundary, which is also extremely unlikely to be chance. Such is the recombinatorial avidity of the genome that we are left with some minor mysteries. Thus, while J and Ed segments appear to reach 217856142 in the Type 5 match, the J/Ed match lower bound only reaches 217856192. It would appear that while GEDmatch only declares a match under certain conditions, eg a small number of missing SNPs, here the J and Ed DNA probably have some mini-segments which mismatch, leading to an excess number of missing SNPs which don't show up in other matches. Thus, the J/Ed match does not quite reach 217856142. Of course, this 217856142 boundary also shows that the 218782054 boundary is not a true lower boundary set by Jeannine. Presumably the recombinatorial avidity of the genome has again created mini-segments which cause GEDmatch to declare or not declare matches depending on how many SNPs are missing, and why it is not possible to rigorously prove IBD by the matches alone - and why we are lucky to have the rare 4-person segment boundaries at 220037666 and 218423580.

Diagrams distilling the above may be found here.

The match details are shown below, using the following colour key:

Precision=7		Precision=3